Brena Yoseltika Indri Wati Mise Aryani Nurfajri RWika Suciaristy Siti Nurjannah 2. Kita sebut cfc suatu titik balik dari grafik f jika f cekung ke atas pada satu sisi dan cekung ke bawah pada sisi lainnya dari c.

Soal Fungsi Kuadrat Y X2 Bx C Memiliki Titik Ekstrim Di 32 14 Jika Grafik Fungsi Tersebut Me
Pada suatu fungsi 𝑓 yang terdiferensiasi dimana-mana maka turunan di titik-titik ekstrimnya adalah nol.

Titik ekstrim fungsi. Dengan demikian titik kritis dari fungsi tersebut adalah 916. Sumbu simetrinya yaitu x3 dan nilai ekstrimnya yakni -1. Ada tiga jenis titik yang bisa jadi merupakan tempat terjadinya nilai ekstrim.
Dari informasi titik potong dengan sumbu X titik potong dengan sumbu Y dan titik ekstrim kita bisa menggambar grafik fungsi kuadrat. Andaikan f didefinisikan pada selang I yang memuat titik c. Sebarang titik dalam daerah asal fungsi yang termasuk ke dalam salah satu dari tiga tipe ini disebut titik kritis.
Titik stasioner suatu fungsi dan jenis jenis ekstrim 1. Klasifikasi bilangantitik kritik a. Nilai Ekstrim Nilai maksimum dari fungsi z fxy dicapai pada pasangan nilai variabel-variabel bebas x dan y.
F x x2 x 6 tentukan titik potong terhadap sumbu x dari fungsi kuadrat diatas. Yakni c berupa salah satu. Titik puncak kurva parabola juga disebut titik ekstrim.
Dari informasi titik potong dengan sumbu X titik potong dengan sumbu Y dan juga titik ekstrim dapat kita gambar grafik fungsi kuadratnya. Jawaban paling sesuai dengan pertanyaan 3. Titik Stasioner Suatu Fungsi dan Jenis-Jenis Ekstrim Kelompok 3.
Dengan demikian terdapat beberapa kemungkinan mengenai bentuk kurva. Tentukan nilai kritis dari. Bisa juga terjadi bahwa suatu nilai maksimum lokal dari suatu fungsi lebih kecil dari nilai minimum lokal dari fungsi tersebut dalam suatu jarak tersebut.
Untuk fx 0 maka. Suatu fungsi tidak harus memiliki nilai minimum atau maksimum pada selang tertentu. Carilah nilai maksimum dan minimum dari f x 4x 3 3x 2 6x 1 pada 21.
Jika f c adalah titik ekstrim maka c haruslah suatu titik kritis. Untuk x - ½ f 12 1 dan fungsi mencapai maksimum. Nilai ekstrim yang terjadi pada ujung selang disebut nilai ekstrim ujung.
Sumbu simetrinya adalah x3 dan nilai ekstrimnya adalah -1. Nilai Ekstrim Fungsi Kuadrat adalah D-4a. Fx 12x 2 6x-6.
Biasanya fungsi yang akan kita cari nilai maksimum dan minimumnya dibatasi oleh suatu selang interval sebagai daerah. Titik kritis tidak terjadi di titik ujung selang 2. Apabila diketahui titik ekstrim suatu fungsi kuadrat maka diperlukan satu titik lagi total dua titik untuk menyusun fungsi fungsi kuadrat tersebut.
Fungsi yt2-5t6 tentukan titik ekstrim dan nilai ekstrim nya. Titik Ekstrim Titik ekstrim fungsi kuadrat fxax 2 bxc yaitu. 0034 Titik Ekstrim Fungsi Dua Variabel Bebas 002.
Selain titik belok sebuah fungsi kubik mungkin pula mempunyai satu titik ekstrim maksimum atau minimum atau titik dua ekstrim maksimum atau minimum. Sebarang titik dalam daerah asal fungsi. Sketsa Grafik Fungsi Kuadrat Parabola.
Walaupun dalam masalah praktis hal ini sangat langka nilai ekstrim dapat terjadi pada titik singular. Titik Ekstrim Titik ekstrim fungsi kuadrat fxax 2 bxc adalah Berarti untuk fungsi kuadrat fxx 2-6x8 titik ekstrimnya adalah sebagai berikut. Turunan kedua f x 12x2 12x 2.
Koordinat titik puncak titik ekstrimtitik stasionertitik balik parabola adalah xp yp dengan. Berikut rumus untuk mencari titik puncak grafik fungsi kuadrat yaitu hitung titik ekstrim di sumbu x lalu hitung nilai fungsinya untuk mendapat titik ekstrim sumbu y. Nilai ekstrim suatu fungsi dapat terjadi pada ujung selang.
Nilai ini didapat ketika x -b2a sumbu simetri. Sebagai contoh pada gambar 1 dan 2 di atas kita dapat melihat bahwa fungsi f x x ² 1 memiliki minimum dan maksimum. Dari pembahasan pada contoh di sub bab sebelumnya didapatkan nilai stasioner fungsi adalah x -1 x - ½ dan x 0.
Tentukan nilai ekstrim dan jenisnya dari fungsi f x x4 2x3 x2 5 Jawab. Ilustrasi berikut akan memperjelas beberapa kemungkinan yang dibentuk oleh suatu fungsi. Hal ini tidak berlaku untuk titik ekstrim.
Apabila diketahui titik ekstrim suatu fungsi kuadrat maka diperlukan satu titik lagi total dua titik untuk menyusun fungsi fungsi kuadrat tersebut. Titik stasioner dari fx 0. Artinya untuk fungsi kuadrat fxx 2-6x8 titik ekstrimnya ialah seperti di bawah ini.
Untuk mengerjakan soal diatas kita akan memplotkan dulu fungsi soal menjadi grafik dalam sistem koordinat tiga dimensi. Fungsi yang mempunyai titik minimum kurvanya berbentuk cembung ke bawah convex downward. Titik Puncak Grafik Fungsi Kuadrat Titik puncak grafik parabola dari fungsi kuadrat dapat dihitung dari bentuk umumnya ax² bx c.
Nilai ekstrim dapat terjadi pada titik-titik stasioner. D b2-4ac Xp absis x titik puncak sumbu simetri absis x saat mencapi nilai max dan minYp ordinat y titik puncak nilai ekstrim nilai stationer nilai max nilai min. Cari titik-titik kritis dari ƒ x x 3.
Garis singgung datar b. Y -7 3x dan y 6 4x c Carilah x jika. Titik ekstrim titik balik pada Y grafik fungsi kuadrat tersebut adalah.
Jika fungsi 𝑓 mencapai ekstrim lokal di 𝑐 dan fungsi 𝑓 terdiferensialkan di 𝑐 maka 𝑓𝑐 0 Sudah sangat jelas. 50 Gambar 28 Kecekungan Grafik Andaikan f kontinu di c. Titik Singuler dari fx tidak ada.
916 termasuk titik kritis karena 916 berada pada 0 dan 4. Nilai maksimum dan Nilai Minimum Fungsi kuadrat. Y x2 10x - 24.
Carilah koordinat jenis dan ketinggian titik ekstrim dari fungsi dua variabel bebas zf xy dibawah. A Tentukan titik ekstrim parabola y x2 4x 2 dan perpotongannya dengan sumbu-sumbu koordinat. Titik singular merupakan titik pada grafik ƒ dalam keadaan sudut tajam garis singgung vertical atau berupa lompatan.
Berikut adalah ketiga tipe titik kritis yang di maksud. Analisis Titik Ekstrim GRAFIK FUNGSI. Garis singgungnya pasti sejajar dengan sumbu x memiliki kemiringan 0 Teorema.
Nilai ini bisa maksimum maupun minimum tergantung pada a. Ada tidaknya titik ekstrim dalam suatu fungsi kubik tergantung pada besarnya nilai-nilai b c dan d di dalam persamaannya. Menyusun Fungsi Kuadrat Bagian III Pada umumnya dalam menyusun fungsi kuadrat diperlukan minimal tiga titik yang dilaluinya.
Untuk x -1 f 1 2 dan fungsi mencapai minimum dengan nilai minimum f -1 -5. Grafik runcing tidak kontinu garis singgung tegak. Titik singular c fc tidak ada.
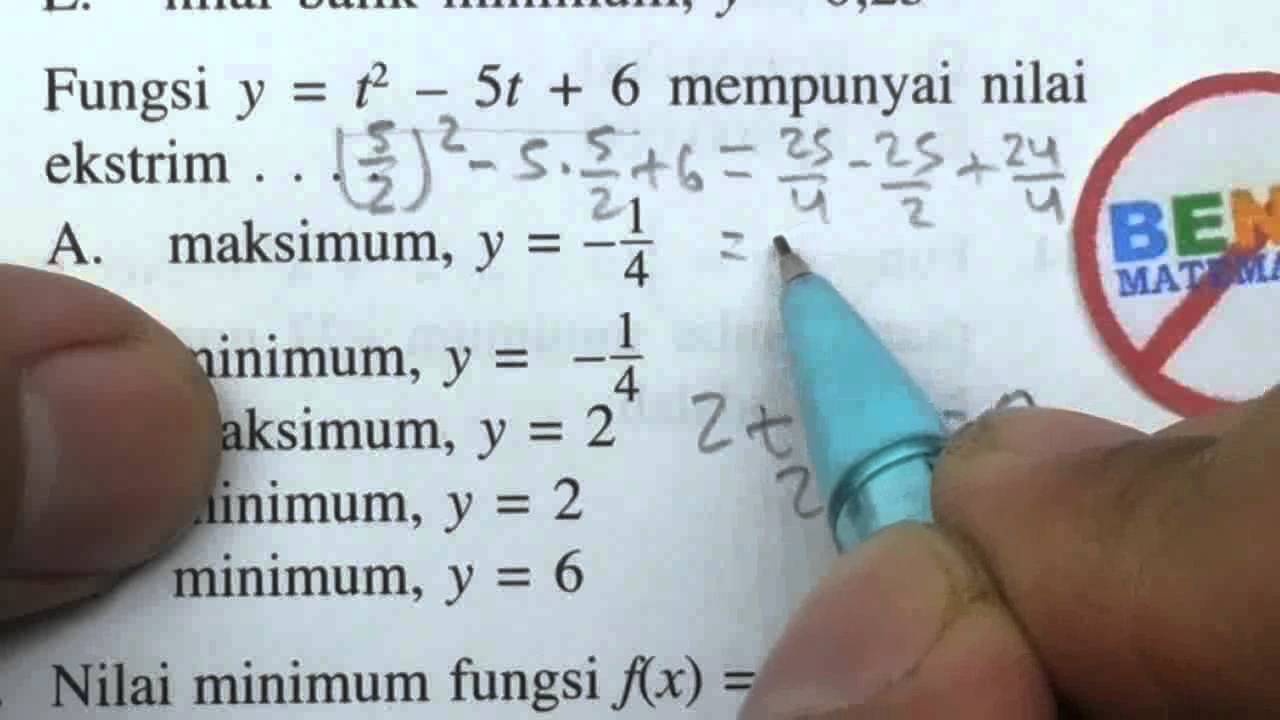
Nilai Ekstrim Diferensial Youtube
Tidak ada komentar