Besar ukuran lingkaran tidak penting. Dengan memakai grid pada gambar di atas kita dapat mengetahui bahwa lingkaran yang berwarna biru memiliki titik pusat di 2 0 dan berjari-jari R 4 satuan panjangSelain itu kita juga dapat mengetahui bahwa lingkaran yang berwarna merah memiliki titik pusat di 2 2 dan berjari-jari r 2 satuan panjang.

Matematika Kelas 8 Unsur Unsur Lingkaran Titik Pusat Jari Diameter Busur Juring Tembereng Youtube
Persamaan lingkaran L adalah.
Titik pusat pada lingkaran adalah. R² x a² y b². Persamaan Lingkaran Definisi Lingkaran Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama dengan titik tertentu. Tempat kedudukan titik A 2 cos θ 2 sin θ apabila θ berubah dari 0 sampai 2π berbentuk.
Pada gambar di atas bagian yang bewarna merah adalah titik pusat lingkaran. Sekarang lanjut ke pembahasan unsur-unsur lingkaran yuk. Berjarak sama disebut jari-jari dan titik tertentu disebut titik pusat lingkaran.
Titik potong dari kedua garis sumbu yang terbentuk pada langkah 1 dan 2 merupakan titik pusat lingkaran. Jadi persamaan lingkaran yang berpusat di titik pangkal dan melalui titik adalah. Jari Jari Lingkaran.
Dalam bab ini akan dibahas bagaimana menentukan pusat dan jari-jari dari suatu persamaan lingkaran. Pada bentuk persamaan x 2 y 2 r 2 lingkaran memiliki titik pusat di O 00 dan panjang jari-jari r. Maka tentukan besar sudut AOB tersebut.
Sudut pusat adalah sudut yang dibentuk oleh titik pusat dengan dua titik yang terletak pada lingkaran sedangkan sudut keliling adalah sudut yang dibentuk oleh tiga. Jangka adalah sebuah alat yang dirancang khusus untuk menggambar dan mengukur lingkaran. Karena lingkaran menyinggung sumbu x dan sumbu y maka jari jri lingkaran adalah 2.
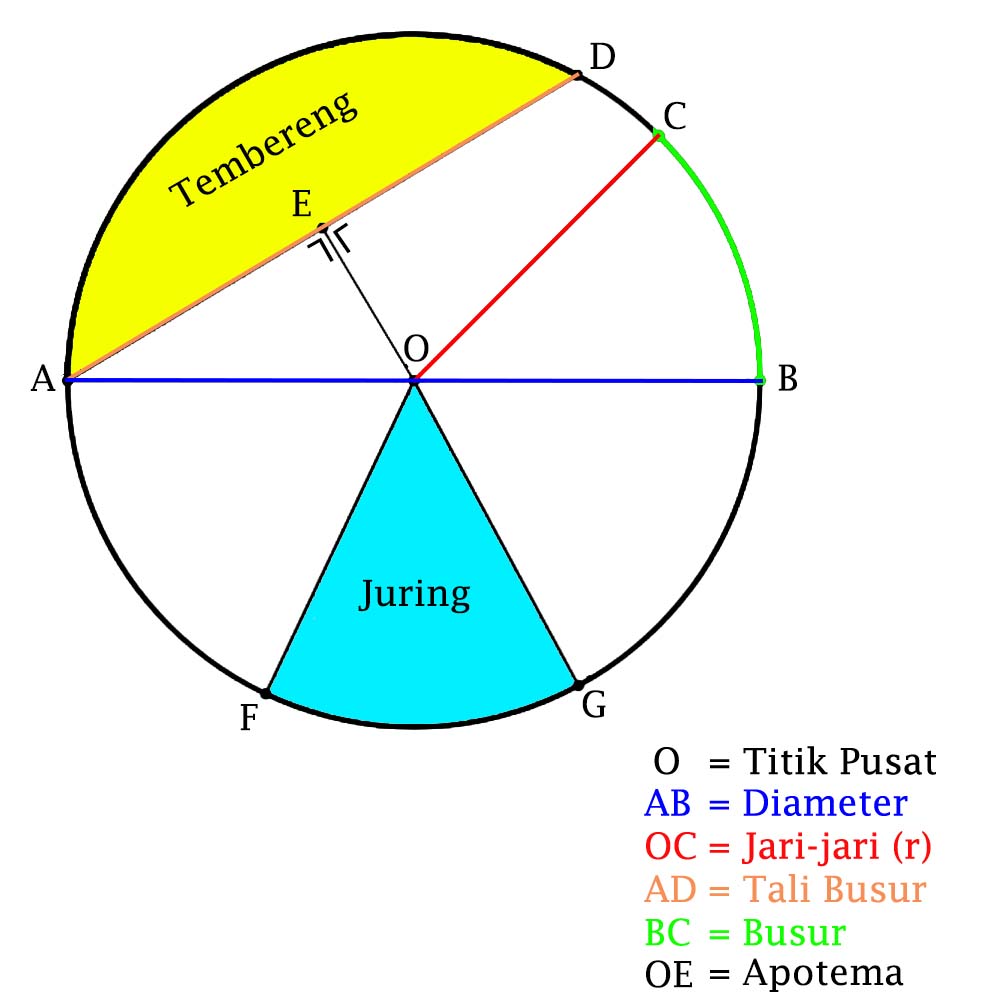
Terdapat beberapa bagian lingkaran yang termasuk dalam unsur-unsur lingkaran diantaranya titik pusat jari-jari diameter tali busur busur juring dan tembereng Agus 2007. Titik tertentu itu disebut sebagai pusat lingkaran sedangkan jarak titik terhadap pusat lingkaran disebut sebagai jari-jari lingkaran. Contohnya pada lingkaran di atas adalah garis OA OC OC OG dan OF.
Nah kumpulan titik-titik tersebut jika dihubungkan satu sama lain akan membentuk suatu garis lengkung yang tidak berujung. Persamaan garis singgung lingkaran x² y² 2x 6y 7 0 di titik yang berabsis 5 adalah. AOB 2 ACB.
Persamaan lingkaran yang berpusat di titik 23 dan menyinggung sumbu x adalah. 15 LINGKARAN Lingkaran adalah suatu kurva tertutup yang terbangun atas kumpulan titik yang memiliki jarak sama terhadap suatu titik yang dinamakan pusat lingkaran ab. Jari-jari adalah jarak titik pusat lingkaran terhadap titik yang berada pada lengkung lingkaran.
Jadi perbedaan utama dari sudut pusat dan sudut keliling adalah elemen pembentuknya dimana sudut pusat dibentuk oleh dua buah jari-jari dan sudut keliling dibentuk oleh dua buah tali busur. Persamaan Lingkaran Berpusat di O00 dan Jari-Jari r OP2 x0 0 2 y0. Perhatikan gambar 22 berikut.
Sedangkan jarak setiap titik pada pusat tersebut dinamakan jari-jari r. Subtitusikan nilai x 5 pada persamaan lingkaran untuk mendapatkan titik singgungnya. Jari-jari lingkaran adalah garis yang ditarik dari titik pusat lingkaran ke arah luar hingga menyentuh garis lengkungUmumnya jari-jari lingkaran disimbolkan dengan simbol r.
Sudut keliling adalah suatu sudut yang terbentuk oleh bertemunya dua buah tali busur. Untuk mempermudah dalam memahami ketiga langkah di atas perhatikan ilustrasi dalam menentukan titik pusat lingkaran berikut. Lingkaran L menyinggung sumbu X menyinggung lingkaran x2y24 dan melalui titik A 4 6.
Gunakan jangka atau jiplak benda yang bundar. 3 kedudukan titik terhadap lingkaran. Contohnya adalah titik O pada lingkaran di atas.
Cara menentukan jari-jari dan pusat lingkaran melalui persamaan standar. Lingkaran adalah kumpulan titik-titik pada garis bidang datar yang semuanya berjarak sama dari titik tertentu. Itulah unsur-unsur yang terdapat dalam bangun datar lingkaran.
X² y² 4x 4y 4 0. Misalkan terdapat suatu titik. Dilansir dari Khan Academy persamaan standar untuk lingkaran yang berpusat di ab dengan radius r adalah sebagai berikut.
Lingkaran dapat dinyatakan memiliki tiga bentuk persamaan umum yang meliputi bentuk x 2 y 2 r 2 x a2 y b2 r2 dan x 2 y 2 Ax By C 0. Secara umum letak titik pada bidang datar. Unsur-unsur ini perlu dipahami agar mudah untuk menyelesaikan permasalahan terkait bangun datar.
Sedangkan letak titik pada sebuah bidang koordinat dinyatakan dalam pasangan bilangan absis dan ordinat. Sudut Pusat pada Suatu Lingkaran. Agar titik 2 m berada di luar lingkaran x 2 y 2 2x - 6y - 15 0 syarat yang harus dipenuhi adalah ketika titik 2 m disubstitusikan ke pesamaan lingkarannya maka diperoleh x 1 2 y 1 2 Ax.
Pembahasan Sudut AOB adalah sebuah sudut pusat yang menghadap pada busur yang sama dengan sudut ACB disebut sebagai sudut keliling. Mari kita pahami dulu definisi dari lingkaran sebagai berikut. Hubungan antara kedua sudut AOB dan ACB adalah.
Untuk persamaan lingkaran yang berpusat di titik pangkal yaitu. Titik pusat lingkaran adalah titik yang terletak di tengah-tengah lingkaran. Dari kedua titik perpotongan tersebut tarik garis sedemikian sehingga memotong lingkaran utama di satu titik c.
Sudut pusat adalah sudut terkecil yang dibentuk oleh pusat lingkaran dan dua titik yang terletak pada busur lingkaran. Titik tertentu ini disebut pusat lingkaran. Dalam ilmu matematika jari-jari dapat diartikan sebagai ruas garis yang menghubungkan titik pusat dengan sebuah titik pada lingkaran atau sebagai ukuran panjang.
Gambar No2 di atas adalah Jari-Jari Lingkaran. Lingkaran terbentuk dari kumpulan titik lengkungan dengan memiliki panjang yang. Pada sebuah lingkaran berpusat dengan titik O perhatikan pada gambar dibawah ini.
Kemudian pengertian lingkaran secara umum adalah satu di antara sekian jenis bangun datar dua dimensi. Persamaan lingkaran yang berpusat di O 0 0 dan berjari-jari 8 adalah. Sedangkan jari-jari lingkarannya adalah r.
Pilihlah satu jawaban yang benar. Sedangkan sudut keliling adalah sudut yang terbentuk antara dua buah tali busur lingkaran dan titik sudutnya berada pada keliling lingkaran. Jika ingin mencari pusat lingkaran yang sudah ada Anda tidak perlu menggambar lingkaran baru.
Gunakan jangka lukis dua buah lingkaran yang kongkruen dengan titik pusat C dan D sehingga lingkaran C dan D saling berpotongan. Maka dapat diasumsikan yang. Maka pusat lingkaran dari persamaan tersebut adalah a b.
Apabila kita perhatikan dalam menentukan titik pusat lingkaran tersebut kita gunakan konsep melukis lingkaran. Belilah di sekolah atau toko alat tulis. Hapus kedua lingkaran yang bertitik pusat di A dan B.
Lingkaran adalah tempat kedudukan titik-titik pada bidang yang yang berjarak sama terhadap suatu titik tertentu. Jari-jari lingkaran dilambangkan dengan r atau biasa disebut dengan radius. Persamaan lingkaran dengan titik pusat berada pada parabola yx2 dan menyinggung sumbu X adalah.
Misalkan lingkaran dengan pusat O dan dua titik A dan B terletak pada busur lingkaran maka sudut terkecil yang dibetuk dari AOB merupakan sudut pusat yang menghadap busur AB. Perhatikan bahwa kedua lingkaran. Menyusun Persamaan Lingkaran a.

Soal Bagian Lingkaran Kelas 6 Sd Diary Guru
Tidak ada komentar